3. t-test

I. t-test 들어가기

1) t-test

모집단의 표준편차가 알려지지 않았을 때, 정규분포의 모집단에서 모은 샘플의 평균값에 대한 가설검정방법

당최 무슨소리냐..? 목적에서부터 들어가보자.

 

2) t-test의 목적

 

t-test의 목적은 "두 집단을 비교하는 것"이다.

 

그런데 여기서 집단이라는 표현이 좀 애매한 부분이 있다. 통계에서 일반적으로 집단은 표본을 이야기하는데 표본만 존재하는 것은 아니다. 모집단이라는 것도 있다.

 

 

현실적으로 모집단을 비교하는 것은 어렵기 때문에 우리는 표본을 추출해서 비교한다.

 

Q. 그렇다면 어떻게 두 집단이 같은지 다른지 비교할까?

A : 두 집단의 표본의 대표값인 평균값이 통계적으로 같은지 다른지를 확인한다!

 

3) t-test를 위한 통계적 질문

예) A대학, B대학의 남학생의 키를 비교해 보자.

• A 대학 남학생의 표본의 평균값 : 178.5cm
• B 대학 남학생의 표본의 평균값 : 179.9cm

이 때, 1) A대학 남학생 평균키(178.5cm)와 B대학 남학생 평균키(179.9cm)가 우연히 같을 확률은 얼마나 될지, 다시 말해 2) A대학과 B대학의 남학생 평균키 차이인 1.4cm가 우연히 발생할 확률은 얼마나 될지 질문하는 것이 t-test를 위한 통계적 질문이 되겠다!

 

=> 그렇다면 과연 1.4cm의 차이가 얼마나 커야 우연히 발생하지 않았다고 판단할 수 있을까? 1.4cm의 차이는 과연 큰 것인가 작은 것인가? 우리는 1.4cm가 얼마나 큰지, 혹은 작은지 알 수 없고, 이 1.4cm가 얼마나 큰지 혹은 작은지 결정할 나름의 비교 대상이 필요하다. 그렇다면, 무엇을 가지고 와서 비교해야 할까?

 

A : 표준편차(분산)

 

• WHY 표준편차?
  • 표준편차가 가진 의미를 다시 생각해보면 각 데이터들이 평균값을 중심으로 떨어져 있는 거리들의 평균이다. 즉, 데이터들이 얼마나 퍼져있는지, 몰려있는지에 대한 판단 기준인 것이다! 이 때 데이터에 큰 문제가 없는 한 특별한 의미없이 우연히 퍼져있는 정도가 된다고도 볼 수 있겠다.
  • 위의 1.4cm의 차이도 결국 두 집단의 수많은 데이터들 사이의 평균적인 거리가 1.4cm라는 의미가 될 수 있겠다.
  • 정리하자면, 두 집단 A와 B의 데이터 사이의 평균적인 거리는 1.4cm이다. 이 때, 두 집단 A와 B의 데이터들의 표준편차가 XXXcm라고 한다면, 만약 이 1.4cm의 차이가 표준편차 XXXcm에 비해 현저히 작은 경우 우리는 이 1.4cm라는 차이에 큰 의미를 둘 수 없을 것이다. 하지만 만약 1.4cm가 표준편차 XXXcm에 비해 현저히 크다면, 우리는 이 평균적인 차이가 어느정도 의미가 있구나, 아 B대학이 A대학보다 평균적으로 유의미하게 크겠구나 라고 말할 수 있게 되는 것이다.

★두 집단의 평균값의 차이가 표준편차보다 현저히 작으면, 우리는 이 차이가 우연히 발생했다고 결론을 내릴 것이다. 반대로, 두 집단의 평균값의 차이가 표준편차보다 현저히 크면, 우리는 이 차이가 우연히 발생하지 않았다고 결론을 내릴 것이다.

 

★이게 무슨말이냐 하면, 표준편차는 데이터 값에 큰 이상치가 있지 않은 이상 우연히 발생한 편차라고 볼 수 있음. 그런데 이 우연히 발생한 편차에 비해서도 현저히 작으면 이 차이는 의미가 없는 차이라는 것이고, 우연히 발생한 편차보다 현저히 크면 이 차이가 의미가 있는 차이가 되는 것.

 

★결론적으로 t-test는 평균값의 차이와 표준편차의 비율이 얼마나 큰지 혹은 작은지를 보고서 결정하는 통계적 과정이다!!

 

---

II. z-test

t-test를 이해하기 위해서는 정규분포로 몸을 풀고 가야 한다. 대부분의 경우 정규분포의 z-test와 t-test를 단순/별도로 설명하지만 연결해서 볼 필요가 있다. 본질적으로 같은 것이기 때문이다.

 

모집단의 경우에는 z-test를 하고 표본의 경우 t-test를 한다. 우리는 모집단을 가지고 test를 할 일이 거의 없기 때문에 t-test가 중요하지만 조금 더 쉬운 z-test를 먼저 이해하고 넘어가보자.

 

1. 정규분포

그래프부터 해석하자면 뮤(평균)를 중심으로 + - 3시그마(표준편차)까지 99.7%의 데이터가 다 포함된다.

• 정규분포의 특징
  • 종모양
  • 정가운데(평균)을 중심으로 좌우 대칭이다.
  • 정규분포의 양 끝은 영원히 0에 닿지 않는다.
• 정규분포는 평균과 표준편차만으로 규정된다.
  • 평균과 표준편차가 다른 무한대 개의 서로 다른 정규분포가 존재한다.
• 정규분포의 아래 면적은 확률을 의미한다.
  • 정규분포 곡선 아래의 모든 면적의 합은 1이다.
  • 따라서 정규분포를 이용한 확률을 구하려면 적분을 해야 한다. (미친 짓이다)

2. 표준정규분포

평균이 0이고 표준편차가 1인 정규분포

 

왜 만들었을까? 표준정규분포를 만들어서 가지수가 무한대인 정규분포 곡선을 적분하는 번거로움을 덜 수 있다.

표준정규분포 사용의 예)

• 금년도 대학교 신입생 1000명을 대상으로 영어 실력고사를 시행
• 영어점수의 분포가 정규분포에 근사
• 평균점수는 82, 표준편차는 5
• 이 때, 82점부터 90점까지의 점수를 받은 학생의 수는?

 

1) 이 상태 그대로 적분하는 것은 어렵기 때문에 정규분포를 표준정규분포로 바꾼다.

 

Z(82) = (82-82) / 5 = 0 , Z(90) = (90-82) / 5 = 1.6

 

 

2) 표준정규분포표를 통해 면적을 구해준다.

 

여기서 1.6에 해당되는 면적(즉 확률)은 0.4452. 다시말해 모집단의 0.4452의 비율만큼 해당된다는 것. 다시 말해 0.4452에 전체 학생 수 1000을 곱하면 문제의 답은 약 445명이라고 할 수 있겠다.

 

이와 같이 z-score(z값)을 가지고 하는 테스트를 z-test라고 하며 z-test는 z값과 표준정규분포표를 이용해 할 수 있다. z-score로 변환하는 것을 z-transformation이라고 하기도 하고 표준화(standardization)이라고 하기도 한다. z-score는 1 표준편차당 관찰값(X)가 평균으로부터 얼마나 떨어져 있는지를 의미하며 z값은 단위로부터 자유롭다. (dimensionless quantity)

 

그런데 이걸 가지고 어쩌라고?

A: 통계적 사고는 어떤 사건이 우연히 발생할 확률이 얼마일지 질문하는 것. 이 때 말하는 확률이 바로 정규분포곡선 아랫쪽의 면적인 그 확률을 말한다.

 

---

III. 양측/단측 검정

A대학의 평균은 178.5cm, B대학의 평균은 179.9cm라고 할 때,

귀무가설(H0)은 A의 평균 = B의 평균, 대립가설(Ha)는 A의 평균 != B의 평균이 될 수 있겠다.

 

이 통계적 가설을 양측과 단측검정으로 확대를 하면,

• 양측검정 : H0 => A의 평균 > B의 평균 || A의 평균 < B의 평균 이 되겠다. 즉, 합집합!

  이 말은 다시, A와 B의 평균의 차이 > 0 || A와 B의 평균의 차이 < 0

  이렇게 단순히 두 개의 값이 다르다, 그래서 의미가 크거나 작다 모두를 포함할 경우, 양측검정이라고 한다.

• 단측검정은 위의 둘 중에 하나만 포함하는 경우. A와 B의 평균의 차이 < 0 이나 > 0 중에 하나만을 채택해서 하는 경우이다.

 

주로 충분한 근거가 없을 때에는 가설을 양측으로, 어느정도 근거가 있을 때에는 단측으로 검정하는 경우가 많다.

 

 

결론적으로 양측검정과 단측검정의 차이는 대립가설의 차이에서 발생한다.

• 양측은 0보다 크거나 작은 두가지를 모두 포함하므로 분포곡선의 양측 꼬리의 면적의 합이 5.0%에 들어갈 만큼 크거나 작아야 한다.
• 단측은 0보다 크다(우측검정)와 0보다 작다(좌측검정)의 두 가지로 나누어 볼 수 있고 어느 한쪽 꼬리의 면적이 5.0%에 들어갈 만큼 크거나 작아야 한다.

 

0을 기준으로 양측이든 단측이든 95% 안에 들어오면 두 평균값의 차이인 Da-b는 우연히 발생한 것이므로 두 집단의 평균값은 통계적으로 같은 것이다.

 

---

IV. t-test 실전

 

우리가 풀어야 할 문제는?

• 귀무가설 : A, B 두 대학의 평균의 차이가 0인지 (즉, 두 집단이 같은지)
• 대립가설 : 두 대학의 평균의 차이 0보다 큰지 or 작은지 (두 집단이 다른지)

 

이제 무엇이 필요할까?

 

z-test를 떠올려보자. z-test를 하기 위해서 필요했던 것은 z-value와 표준정규분포였다.

 

따라서 우리는 이제 t-value와 t-분포가 필요할 것이다. 한번 더 기억하자면 t-test의 목적은 두 집단이 같은지 다른지 알고자 하는 것이다. 그래서 통계적 가설에 의거해 두 집단의 평균값의 차이가 0과 같은지 다른지 궁금하다.

 

 

위의 값에서 우리가 궁금해하는 차이는 분자에 있다. 여기서부터 중요한 것이 통계적인 생각, 질문, 접근법이다. 도대체 저 값이 얼마야 커야 큰 것일까? 알기 위해서는 비교 대상이 필요하겠다.

 

그 비교대상으로써 표준편차가 있다고 했다. 표준편차는 우리의 데이터가 평균값을 기준으로 평균적으로 퍼진 정도이다. 따라서 이 자체는 의미 없는(우연히 발생한) 편차이다. 만약 두 집단의 평균값의 차이가 의미 없는 편차인 표준편차만도 못하다면, 당연히 이 차이는 우연히 발생했다고 보아야 할 것이다.

 

이 때, 표준편차를 루트 n으로 나누는 분모에서 루트 n의 역할은 무엇일까?

 

데이터의 개수가 증가할수록 df(자유도=데이터의 개수-1)도 증가한다. 또한 df가 증가할수록 t-분포 곡선이 점점 표준정규분포에 가까워진다.

 

 

즉, 우리가 데이터를 많이 모을수록 t-분포는 표준정규분포에 근사한다는 것. n이 커지면 분모는 작아지고, 분모가 작아지면 t-value가 커지고 t-분포는 표준 정규분포에 근사한다. 자유도가 커진다는 의미는 우리가 t-분포에 묶여있다가 자유롭게 표준정규분포를 사용할 수 있음을 의미한다.

 

만약 표준편차(s)가 7.05cm였고, 표본의 크기(n)가 101명이라면 t값은 약 1.996이 되겠다. t값을 구하면 t-table의 two-tails에서 자유도와 0.05에 해당되는 확률을 찾아 비교하면 된다.

 

 

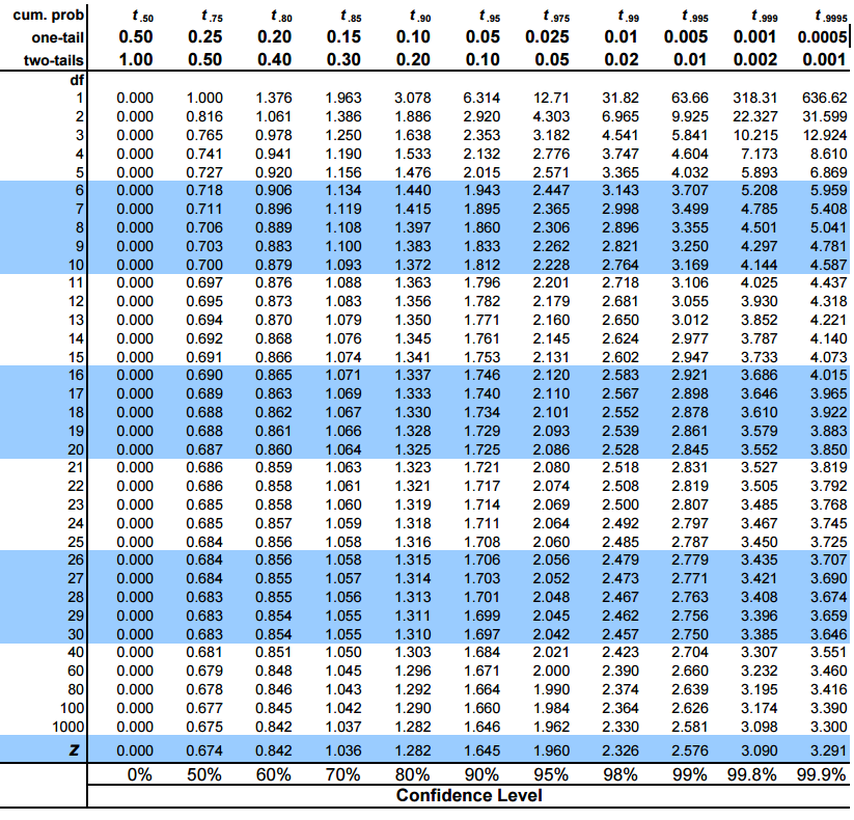
여기서 찾은 숫자(1.984)를 critical value라고 하는데, 이 critical value를 어디에 쓰느냐?

 

 

1.984라는 값은 자유도 100일 때, 우연히 발생할 확률 95%의 끝 점에 해당되는 값이다. 그런데 1.996은 1.984보다 크고, 이 말은 우연히 발생할 95%의 영역보다 위쪽 영역, 즉 우연히 발생하지 않았을 영역에 해당된다는 말이다.

 

정리하자면, 표준편차(s)가 7.05cm, 표본의 크기(n)가 101명이라면, t값은 1.996, df(자유도)는 100이 되고, critical value는 1.984가 된다. 그런데, 우리의 t값이 c.v보다 크므로 두 평균의 차이인 1.4cm가 우연히 발생했을 확률이 5%보다 작으므로, 이 차이는 통계적으로 유의하다고 할 수 있겠다.

 

그러므로 두 대학의 남학생의 키는 통계적으로 유의하게 다르다. 이 뜻은 두 대학 학생의 평균키 차이인 1.4cm가 우연히 발생했을 확률이 5%보다 작으며, 이는 우연히 발생했다고 보기 어려워(현재로서는 정확한 이유는 모르겠으나) 두 대학의 학생의 키가 다른 뭔가 원인이 있다고 볼 수 있다.

 

주의할 점은 이렇게 유의하다고 하고 결론을 내는 것이 아니고, 그 다른 원인이 무엇일지 찾아보는 과정으로 이어져야 한다는 점!

 

---

VI. t-test의 종류

 

1) Two-sample t-test

: 두 집단의 평균값이 다른지 비교

 

2) One-sample t-test

: 한 개의 샘플을 가지고, 그 샘플의 평균값이 통계적으로 특정 수치와 같은지 다른지 검증하는 것. 가령, X대학의 평균키가 178.5cm라고 할 때 이 수치가 180cm라는 수치와 같다고 볼 수 있는지 아닌지 (이 때 180cm는 연구자가 임의로 설정한 값일 수 있고 대한민국 전체평균키일 수도 있다)

 

3) Paired t-test

: 한 개의 샘플을 시간적으로 다르게 평균값을 비교하는 것. 가령, 어떤 집단에서 시험 점수를 비교한다고 할 때, 기존 교재로 학습했을 때의 점수와 새로운 교재로 바꿔서 학습한 이후의 점수를 비교하는 것. 이 때, 사용하는 t-test의 공식은 다르다.

 

 

출처 : 유튜브 Sapientia a Dei

Sapientia a Dei

진짜 너무너무 감사합니다.. 통계가 재밌어질 줄이야..ㄷㄷ